One article understands the Fourier transformation knowledge! ! !

First, time domain and frequency domain

The time domain is changing rapidly, and the frequency domain is constant.

Fourier first had a very advanced idea in his era. All waves were composed of sine waves of different amplitudes, frequencies, and phases. At that time, his teachers included dissenting opinions. Simple, you take the sinusoids of the lines to give me a straight square wave and a triangular wave.

Fourier then came up with a Fourier transform (FT) to prove that square waves and triangular waves can be mathematically combined with sine waves, but there was no physical proof at the time.

With the rise of the European industrial revolution, especially the culmination of image processing technology in recent decades, people are now not to prove their authenticity, but to use this tool to handle all kinds of applications. Let's just say, FT is to deal with "wave", and "wave" is a kind of signal, so as long as it involves the signal level, FT can play a certain role.

The essence of FT is that the periodic continuous signal in the time domain can be superimposed on the frequency domain by sine waves of different frequencies and amplitudes. We illustrate this problem by the following figure. For example, if a square wave is contrasted by different numbers, different frequencies, and different amplitudes, we can get a preliminary understanding of FT.

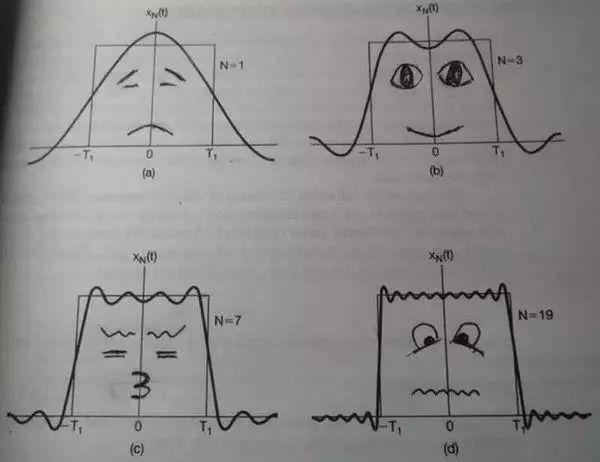
Different amount of superimposed effect

The first picture is a depressed sine wave cos(x);

The second picture is the superposition of two sinusoidal waves of cos (x) + a.cos (3x);

The third figure is a superposition of four sine waves that spring;

The fourth picture is a superposition of 10 constipation sine waves.

Instead of seeing more sine waves, the superimposed waveforms increasingly conform to the original square wave. So, if it is an infinite sine wave to superimpose it?

Second, the Euler formula

Straightforward, whether you remember or not, I first put out the Euler formula.

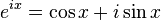
The concept of imaginary i was touched in high school, but then we only knew that it was the square root of -1, but what is its real significance?

Here is a number axis with a red line segment on the number axis. Its length is 1. When it is multiplied by 3, its length changes and becomes a blue segment. When it is multiplied by -1, it becomes a green segment, or the segment rotates around the origin on several axes. 180 degrees.

We know that multiplying -1 is actually multiplying i twice to rotate the line by 180 degrees, then multiplying by i - the answer is simple - rotates 90 degrees.

At the same time, we obtained a vertical imaginary axis. The real and imaginary axes together form a complex plane, also known as a complex plane. In this way we understand that one function of the imaginary number i is rotation.

Real and imaginary axes

Before learning the complex function, we were exposed to a real number; the complex function is an extension to the imaginary number, and Euler's formula is a bridge for this extension. Not just FT, it also plays a key role in many areas.

Third, the nature of FT

The essence of FT is mentioned above. The following diagram shows the time domain and frequency domain in a large coordinate system. Then the formula of FT becomes the magnitude of the sine of these different amplitudes. Because their frequency changes regularly based on the original time domain waveform, the frequency is known. At the same time, there is a DC component that is derived to meet the amplitude of the original waveform. Get these, that is to complete the entire FT.

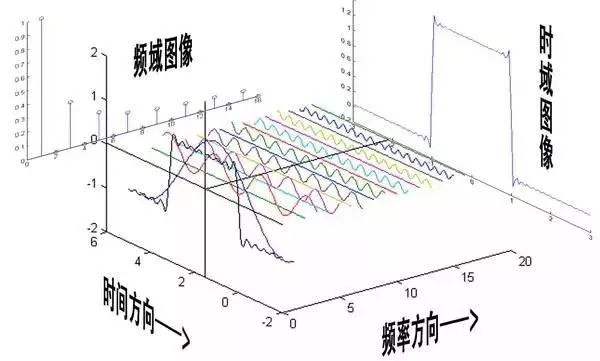
The nature of FT

FT formula:

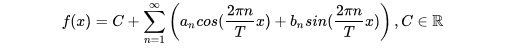
Where C is the dc component mentioned above, an and bn are the sine amplitudes of different frequencies.

Finally, it should be noted that FT is the basis of DFT and FFT. As long as the essence of FT is mastered first, the latter two are only the specific application and implementation forms of FT.

Nintendo Switch Steering Wheel

[Pals & Family Fun]2 steering wheels and 2 grips compatible with Nintendo Switch, 4 Player on match, who will be the winner and prankster?
[Less on Weight & Heavy on Quality] High Quality ABS material makes it sturdy and smooth, comfortable and easy handle.
[Easy Install and Uninstall]Each grip and wheel is compatible with any color, and you can easily install with "+" and "-" instruction on grip, uninstall without 3 second.
[Sentive & Protective]It can be accurate to ports and buttons, curved palm design reduces hand fatigue and increases comfortable to hold

[Enjoy the Game]Perform your better skill on racing games, catch your pals' eyes, or become a prankster to delivering happiness.

Product Name	For Nintendo Switch hand grig and steering wheel kit
Material	ABS
Product size	hand grip:15.592.8CM Wheel:13.813.83 CM
product net weight	Hand grip:47.4g /pcsWheel:77g/pcs
collor	black, pink and blue,red and green,yellow and brown or OEM
package	Gift Box
packing list	2hand grip+2 Steering wheel
OEM/ODM	warmly welcome
Advatage	4 Pack in one box, multicolor to choose
samples time	1-2day
Packing detailes	28pcs/CTN , NW:11KG Gross weight:12 KG Means:564732.5cm
warranty	1 year

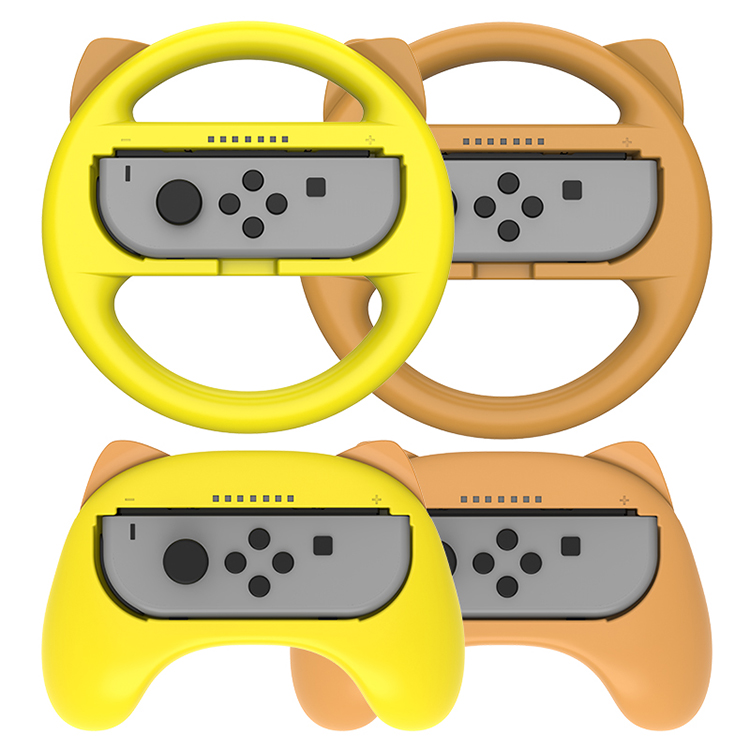
Nintendo Switch Steering Wheel,Grip For Nintendo Switch Controller,Nintendo Switch Controllers Grip Kit,Switch Racing Steering Wheel

Shenzhen GEME electronics Co,.Ltd , https://www.gemesz.com