How does Inertial Positioning Solve the Problems of Gyro Drift and Magnetic Field Disturbance?

For the attitude calculation of the navigation system, when integrating the gyro and the electronic compass, the integral error and magnetic field interference are respectively present. Therefore, the Kalman filter and the complementary filter are used for positioning. Firstly, the electronic compass and gyro are used to obtain the optimal estimated quaternion by Kalman filtering. Then, the complementary filter algorithm is used to compensate the gyro drift to obtain the corrected quaternion. The quaternion and Kalman filter obtained this time are obtained. The optimal quaternion is obtained and the quaternion is again optimally estimated by the Kalman filter, and then the attitude angle is output. The experiment compares the effects of the algorithm and the complementary filtering algorithm and no filtering algorithm. Experiments show that the algorithm can not only effectively solve the problem of azimuth error divergence, but also effectively solve the magnetic field interference problem and achieve high-precision azimuth output.

With the development of miniaturized inertial devices represented by MEMS (Micro-electromechanical Systems) sensors, inertial positioning technology based on Strapdown Inertial Navigation Principles and MEMS sensors has also received increasing attention, especially in indoor rooms where it is difficult to receive satellite signals. Underground, mine, underwater, battlefield and other occasions [1]. In view of the above problems, the method of correcting the gyro by using an electronic compass is often used, and the magnetometer is more susceptible to interference in indoor, underground, mines, underwater, and the like, resulting in a greater azimuth deviation. Many fusion algorithms have emerged for the magnetometer's vulnerability to interference and gyro-integral drift problems, such as Kalman filtering, Unscented Kalman Filtering (UKF), Extended Kalman Filtering (EKF), etc. [2-4]. The filtering method needs to establish an accurate state equation and observation equation. There is also a kind of filtering algorithm that is extended on the basis of complementary filtering, such as classical complementary filtering, complementary filtering algorithm based on gradient descent method [3-6], but the accuracy of this filtering algorithm is not high. In the face of these problems, this paper proposes an inertial localization algorithm that combines Kalman filtering and complementary filtering. In the design of Kalman filtering, the quaternion derived from the fusion of accelerometer and magnetometer is used as the observation value, and the gyroscope is used. The resulting quaternion is used as the state value, filtered through data fusion to complete the first optimal estimation of the quaternion, and the gyro drift is compensated for the gyro drift by using the designed complementary filter to obtain the corrected gyro drift. The angular velocity, then the quaternion that is continuously updated after correction, and then the first estimated optimal quaternion is estimated by the second Kalman filter, and then the high-precision attitude angle is output.

1 overall design of the algorithm

The general idea of ​​the inertial localization algorithm based on Kalman filtering and complementary filtering is shown in Figure 1.

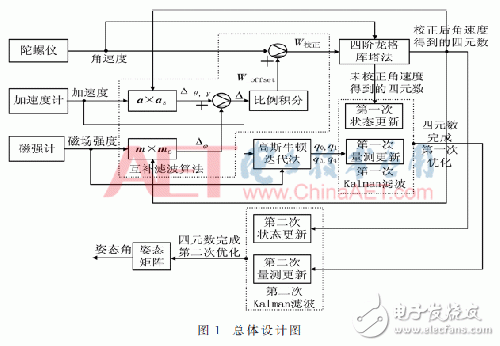
First, the quaternion of the magnetic field intensity and acceleration measured by the magnetometer and accelerometer using the Gauss Newton iteration method is sent to the Kalman filter as the observed value, and the angular velocity value measured by the gyroscope is used as the fourth-order Kuta method. The quaternion solved is used as the Kalman filtering state value to obtain the first optimal estimate of the quaternion. In the Kalman filter process, random noise can be removed, and the gyroscope can be corrected through the electronic compass, and the gyro can be avoided. Disturbance data from magnetic field interference.

Next, using the transformation matrix between the carrier coordinate system and the geographic coordinate system, the gravity and geomagnetic components in the geographic coordinate system are converted to the carrier coordinate system, and then the accelerometer and the magnetometer are measured in the carrier coordinate system. Performing a vector product operation with the magnetic field strength, adding the sum of the product of the two together through a proportional integral low pass filter, the high frequency jitter signal in the electronic compass measurement attitude can be filtered out, and then fused with the angular velocity measured by the gyroscope. The angular velocity compensated by the gyroscope is obtained, and the corrected quaternion is obtained by using the fourth-order Runge-Kutta method.

Finally, the corrected quaternion obtained by the complementary filter algorithm is used as the state quantity. The second quaternion is optimized by using the optimal quaternion obtained from the first Kalman filter as the observation measure, and then the second optimization of the quaternion is performed. The quaternion is used to establish the attitude matrix to obtain a more accurate attitude angle.

2 Kalman filter design

Kalman filtering is an algorithm that uses the state equation of the linear system to input and output observation data through the system to make an optimal estimation of the system state. Establishing the system's state equations and measurement equations is the main task of Kalman filtering. In this Kalman filter design, the constant amount of quaternion update is used as the state quantity in the Kalman filter.

Set up the measurement equation below, by the gravitational acceleration and the triaxial accelerometer

In the formula (4), ax, ay, and az represent the measured values ​​of the gravitational acceleration, and the gravitational acceleration is represented by g.

The relationship between the geomagnetic field and magnetometer measurement information results in:

The quaternion is obtained from the equations (6), (7) and the Gauss-Newton iteration method as observations. The measurement is taken as:

Equation (8) mesoscopic equation Z(k) = H(k)X(k) + V(k), where H(k) is the observed gain matrix, V(k) is the observation noise, and the variance R ( k) Can be obtained from the sensor's measurement data. Since both the first Kalman filter and the second Kalman filter are optimal estimates of the quaternion, the above filtering formula and the established equation remain unchanged.

3 complementary filter algorithm design

Because the azimuth angle obtained by integrating the gyroscope has a long time error product, its dynamic response is good and it is not susceptible to external interference. The corresponding electronic compass is vulnerable to external interference, but it has the advantage of no error accumulation. Complementary filtering is to use the high-frequency characteristics of the gyroscope and the low frequency characteristics of the electronic compass to fuse, and adjust the frequency characteristics through the proportional link, as shown in Figure 2.

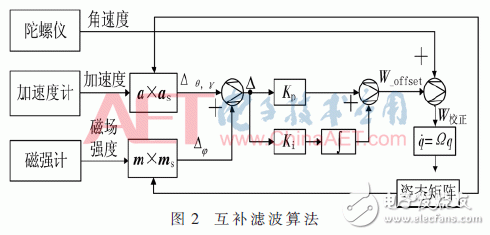
In FIG. 2 , a and m represent acceleration and magnetic field intensity measured by an accelerometer and a magnetometer in a carrier coordinate system; a posture conversion matrix formed by a quaternion of a gravity component and a geomagnetic component in a geographic coordinate system is transformed into a carrier. The gravity and geomagnetic components in the coordinate system are denoted by as and ms respectively. In the carrier coordinate system, the product of a, as, m, and ms is subjected to a vector product, and the calibration errors of the accelerometer and the magnetometer to the gyroscope are obtained. The errors of the pitch and roll angles are set to Δθ, γ, and the error of the azimuth angle is set to ck5-gs8-x1.gif:

The final angular velocity is solved through the fourth-order dragon Gekota method to obtain the optimal attitude angle.

4 Experimental verification and result analysis

This article uses MPU9150 module to verify the test, through the hardware I2C bus to read data, the sensor according to 100 Hz / s data update, external interrupt data acquisition, and then the collected data stored in TF, through MATLAB programming for data calls. In order to verify the effect of this inertial positioning fusion algorithm, the test is mainly conducted in two modes of severe walking and magnetic field interference, and both methods are completed indoors. Figure 3 is to carry the sensor personnel (the sensor is tied to the foot) in a certain position in the room, turn around to the starting position, the length of about 5 min; Figure 4 is to carry the sensor personnel to maintain the standing posture during the next elevator test . In Fig. 3 and Fig. 4, a single gyro solver (no filter algorithm) is represented by (a), and a complementary filter algorithm is represented by (b), and this algorithm is represented by (c).

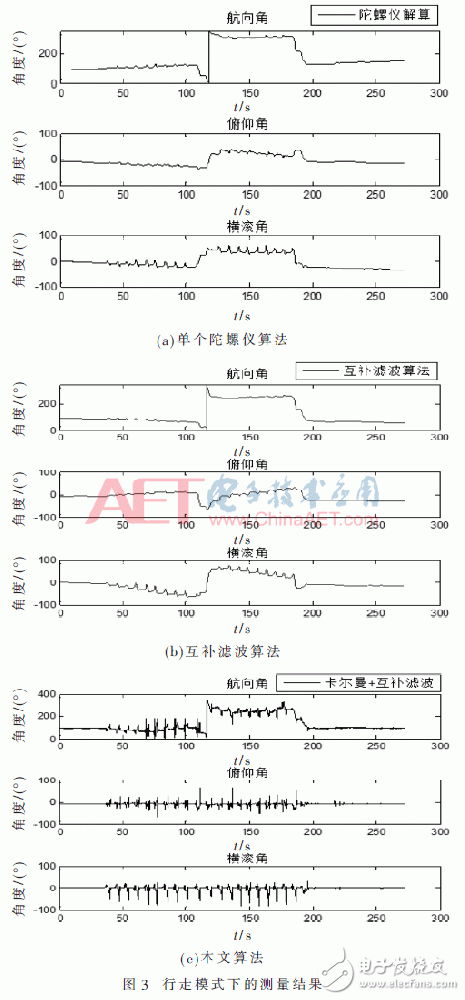
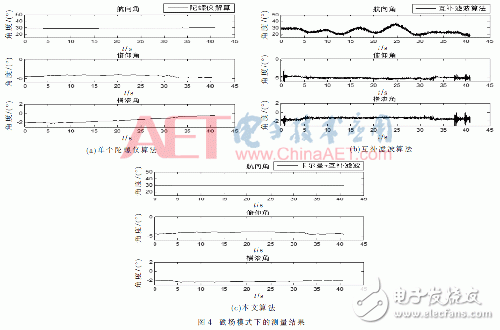
Comparing the data of the azimuth deviation at the beginning and the end of Fig. 3 shows that the complementary filter algorithm is more accurate than the single gyro to perform the pedestrian orientation calculation, but the position offset of the complementary filter algorithm is within 8°, and the algorithm runs about 5 min. Starting position deviation is within 1.5°. From Fig. 3(c), it is proved that this algorithm can accurately provide the orientation under large dynamics (circling). From Fig. 4, we can see that in the case where the magnetometer in the elevator is strongly interfered with, only the complementary filter algorithm will solve the problem of more serious azimuth deviation than the single gyro, and the inertial positioning using Kalman filtering and complementary filtering is integrated. The algorithm avoids this problem, ensures that the attitude accuracy is within 2°, effectively suppresses the magnetic field intensity interference, and ensures the azimuth high-precision output.

5 Concluding remarks

This paper proposes an inertial localization algorithm that uses Kalman filtering and complementary filtering to solve the problem of integral deviation of gyroscope and magnetometer susceptible to interference in navigation solution. The Kalman filter is used to find the optimal quaternion. Complementary filtering corrects the angular velocity of the gyroscope, updates the quaternion by the corrected angular velocity, and uses the Kalman filter to find the optimal quaternion for the two corrected quaternions. Through the experimental results, we can see that this method can not only solve the gyro drift problem, but also can effectively suppress the magnetometer interference problem, can accurately calibrate the azimuth, and achieve a stable and high-precision attitude angle output.

Perkins 201-400KW Diesel Generator

201-400KW Diesel Generator,Perkins Soundproof Generator,Perkins Super Silent Type Diesel Generator,Perkins Super Silent Power Generator

Shanghai Kosta Electric Co., Ltd. , https://www.ksdpower.com