In designing a microcontroller program, it is often necessary to use an ADC to acquire an external analog signal. There are some signals we are more concerned about its DC and low-frequency components, in order to filter out high-frequency noise, we need to use low-pass filter.
A common way of implementing low-pass filters using electronic circuits is first-order RC passive filters. In simple terms this is:
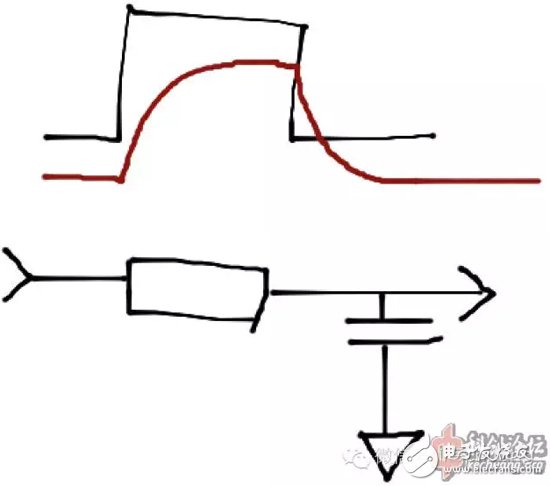
All kinds of calculation of RC filter are slightly, there is a need to please Google.
The RC filter has many disadvantages for the microcontroller's ADC input. If the value of R is small, C is required to be large, and the input signal impedance cannot be too large; if the value of R is large, the charge released by the ADC sampling instantaneously will make the port voltage rise and cannot be released within the sampling time. To a stable level. This can cause sampling accuracy problems.
Even if one op amp is used to buffer the output of the RC filter and then connect to the ADC, it only solves the input impedance problem. The ADC circuit will still produce noise in the conversion result due to outside interference. Therefore, we hope to use the program to implement low-pass filtering inside the microcontroller and completely eliminate high-frequency noise.
Digital low-pass filters come in two forms, IIR and FIR.
IIR is an infinite impulse response filter. Its characteristic is that the output is related to the input of an infinite amount of time ago. This is similar to the response of the RC filter above. As time passes, the output voltage will only be infinitely close to the input voltage and not equal to.
Implementing IIR low pass with C language is very simple:
Int last = 0;
// The following function operates at a fixed frequency and the output of the function is the output of the IIR low-pass filter.
Int lowpass()
{
Int this = ADC();
Last = (this * 1 + last * 15) / 16; // the new last is the old last * 15 / 16 + this * 1 / 16
Return last;
}
If you graph the function return value, the resulting waveform will be the same as the RC filter waveform. To change the cutoff frequency, simply change the composition of the new last in the second sentence of the function (for example, change to 3/4 and 1/4 and the cutoff frequency will increase).
It is worth noting that the above code uses integer multiplication and 2 n-th power division, so after compiling optimization, it runs ultra-fast on 8-bit platform. If you use a platform with a floating-point arithmetic module, use floating-point numbers directly.
The IIR feature is memory saving. The filter above uses only two variables.
The disadvantage of IIR is instability. If you change 15 to 17, it is clear that the output of this filter will overflow after some time. You must be responsible for ensuring that the IIR filter is stable.
FIR is a finite-impulse-response filter. Its characteristic is that the output is related to the input that has been limited for a long time (a period of time). Since the sampling in the digital system is discrete, the number of samples in each period of time is fixed. Therefore, each output value of the FIR filter can be obtained by calculating the previous fixed number of samples. In particular, FIR filters are often used in FPGA-based digital signal processing systems because the calculation of a fixed number of sampled values ​​can be implemented in parallel in the FPGA circuit. In contrast, the IIR filter does not rely on previous sampling, but relies on the previous filter state (existing feedback), so in most applications that are more complex than first-order low-pass filters, the IIR filter has no FIR characteristics. Stability (for stability, high computational accuracy), slower computation than FIR, and no universal design.
Below I use c language to achieve a simple FIR low pass. We add up the last 8 sampled values ​​and average them as output.
Int buf[8];
Int lowpass()
{
Int k = 7;
While(k--)
Buf[k] = buf[k-1]; // Move buf[6] to buf[7], buf[5] to buf[6], etc. to free buf[0]
}
Buf[0] = ADC();
Return (buf[0] + buf[1] +...+ buf[7]) / 8;
}
The temporal image of this filter looks a bit like this:
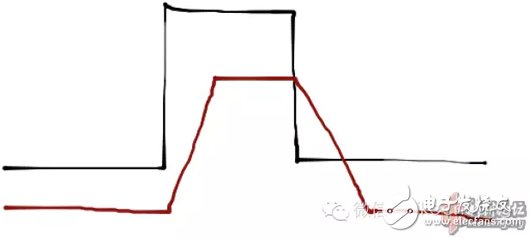
It is worth noting that the above function can be further simplified to speed up the calculation. The above filter has another name: a moving average filter, which most investors should be familiar with.
Although the time domain image is beautiful, the frequency domain image of this filter is not beautiful at all:
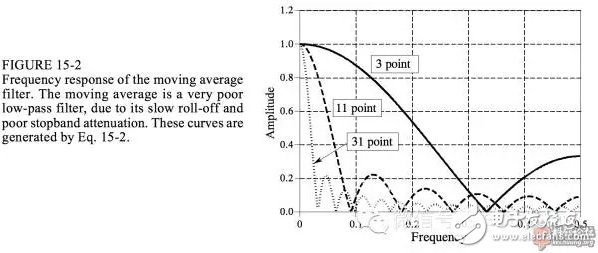
It can be seen that as the number of points increases, the image seems to shrink from right to left, and the suppression of high frequencies is not good.
So if you want to get a better low-pass effect, you shouldn't increase the number of points, but you should use multiple identical FIR filters in series (one output is the next input).
Note: Pass is a "pass" and means the number of iterations.
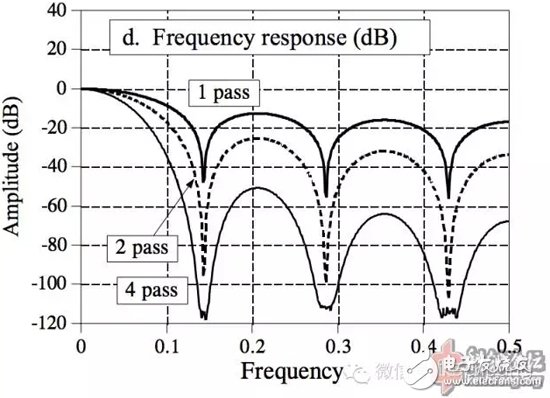
The above is the amplitude frequency response used in series. The time domain image is also very beautiful:
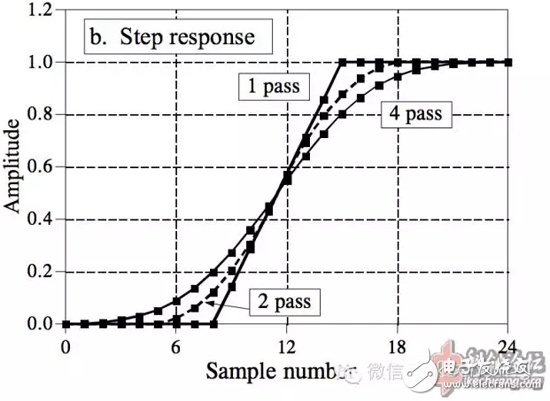
The end of the paper gives the information found at the time of writing this article. Everyone must learn to use Google to search for English keywords, because foreigners are more serious and open than we are to knowledge.
Just the moving average filter, the time complexity is O(n) (set n samplings at a time).
Can be optimized to O(1) form:
Int buf[8];
Int k=0;
Int result=0;
Int lowpass()
{
Result -= buf[k];
Buf[k] = ADC();
Result += buf[k];
k = (k + 1) % 8;
Return result;
}
Breakout Cable,Indoor Breakout Fiber Optic Cable,Fiber Optic Breakout Cable,Pvc Optical Breakout Cable
ShenZhen JunJin Technology Co.,Ltd , https://www.jjtcl.com