Development of virtual function applications, greatly reducing development time

Recently, Professor Zhou Ligong has published his painstaking work "Programming and Data Structure" for several years. The electronic version has been distributed to electronic engineers and college groups for free download. Authorized by Professor Zhou Ligong, the content of this book is serialized.

> > >> 1.1 virtual function

> > > 1.1.1 Binary Tree

Tree is widely used, for example, the database is constructed from the tree, C compiler lexical analyzer is parsed by the generated tree.

A tree is a data structure that manages data like the relationship between a tree trunk, a tree branch, and a leaf. Usually, a tree has a trunk from the root , and then some branches grow from the trunk, and then a smaller branch grows on the branch. The leaves grow on the thinnest branches, and the data structure of the tree is like a tree that is inverted by a tree.

A tree is made up of nodes (vertices) and branches, with a node as the starting point. This starting point is called the root node of the tree. A few branches can be connected from the root node, each branch is connected to a node, and the extended nodes can continue to extend new nodes through the branches. The old nodes in this process are called parent nodes, and the new nodes that are extended are called child nodes, and the nodes that are not in one child node are called leaf nodes. In addition, the number of branches that pass through the root node to reach a node is called the depth of the node.

From the family relationship of genealogy trees, the genealogical tree makes it easier to introduce the terminology used to describe tree structure in computer science. Every node in the tree can have several children, but only one parent. The meaning of ancestors and grandchildren in the tree is exactly the same as in everyday language.

In contrast to the roots are nodes without children, these nodes are called leaves, and nodes that are neither roots nor leaves are called internal nodes, and the length of the tree is defined as the length of the longest path from root to leaf. (or depth). In a tree, if the length of each path from root to leaf is roughly equal, then the tree is called a balanced tree. In fact, it is very complicated to achieve a tree that can always guarantee a balance, which is why there are many different kinds of trees.

In fact, each level of the tree is a bifurcation form. If a node in the tree and its subtree are arbitrarily selected, the obtained part conforms to the definition of the tree. Each node in the tree can be seen as the root of the subtree rooted at itself, which is the recursive nature of the tree structure. If the tree is examined from a recursive point of view, then the tree is just a collection of nodes and a subtree attached to it - in the context of a leaf node the set is empty, so the recursive nature of the tree is its underlying representation and most The basis of the algorithm for tree operations.

An important subclass of the tree is the binary tree, which is a commonly used tree data structure. Each node of the binary tree has at most two child nodes (left and right), and the nodes other than the root are either the left child of the parent node or the right child.

> > > 1.1.2 Expression Math Tree

Problem

Solving an arithmetic expression is a binary tree whose nodes contain two types of objects: operators and final values. An operator is an object that has an operand, and the final value is an object that has no operands. The idea behind the expression tree—stored in the parent node is the operator whose operand is composed of subtrees that extend from the child nodes. The operands may be final values, or they may themselves be other expressions. The expression is expanded in the subtree, and the final value resides in the leaf node. The advantage of this organization is that an expression can be converted into three common representations by expression: prefix, infix, and suffix, but The infix expression is the most familiar expression learned in mathematics. Here, the 2*(3+4)+5 infix expression arithmetic tree structure will be taken as an example.

First, split "2*(3+4)+5" into the left subtree and the right subtree , where "+" is the root node and the value of the left subtree is 2*(3+4), the right subtree The value is 5; then 2*(3+4) is split into a left subtree and a right subtree, where "*" is the root node, the value of the left subtree is 2, and the value of the right subtree is 3+. 4; then split 3+4 into a left subtree and a right subtree, where "+" is the root node, the value of the left subtree is 3, and the value of the right subtree is 4, as shown in Figure 4.6 . Note that no knowledge of parentheses or operator precedence is required in the representation of the tree because the computational process it describes is unique.

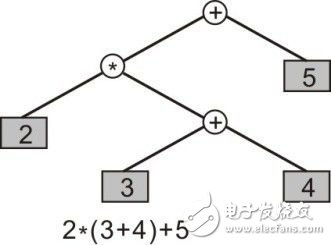
Figure 4.6 Expression Math Tree

It can be seen that from the root node to the leaf analysis , the nodes of the expression arithmetic tree are the arithmetic operators "+(Additive)" and "*(Multiplicative)", and its leaves are operands (Number ) . Since all operations here are Binary, that is, there are at most two children per node, this particular tree happens to be a binary tree. So you can calculate (calculate, abbreviated as calc) each node in the following way:

● If it is a number, return its value;

● If it is an operator, the values ​​of the left and right subtrees are calculated.

The calculation process is to input 3 and 4 respectively, then calculate 3+4; then input 2, then calculate 2*(3+4); then input 5, and finally calculate 2*(3+4)+5.

The traditional approach is to define a struct _Node that contains binary operators and numeric nodes. See Listing 4.12 for details .

Listing 4.12 arithmetic expression tree interfaces (calctree.h)

1 #pragma once

2

3 #define NUM_NODE 1

4 #define ADD_NODE 2

5 #define MULT_NODE 3

6

7 typedef struct _Node{

8 int type;

9 double val;

10 struct _Node *pLeft;

11 struct _Node *pRight;

12 }Node;

13

14 double Calc(Node * pNode);

15

16 #define newNumNode(val) {NUM_NODE, (val), NULL, NULL};

17 #define newAddNode(pLeft, pRight) {ADD_NODE, 0, (pLeft), (pRight)};

18 #define newMultNode(pLeft, pRight) {MULT_NODE, 0 , (pLeft), (pRight)};

The structure is initialized using macros named newNumNode, newAddNode, and newMultNode. The implementation of the expression arithmetic tree interface is shown in Listing 4.13 .

Listing 4.13 implement arithmetic expression tree interface (cacltree.c)

1 #include"Node.h"

2

3 double Calc(Node * pNode)

4 {

5 double x = 0;

6 switch (pNode -> type){

7 case NUM_NODE:

8 x = pNode -> val;

9 break;

10 case ADD_NODE:

11 x = Calc(pNode -> pLeft) + Calc(pNode -> pRight);

12 break;

13 case MULT_NODE:

14 x = Calc(pNode -> pLeft) * Calc(pNode -> pRight);

15 break;

16 default:

17 break;

18 }

19 return x;

20 }

An example of the use of an expression arithmetic tree is shown in Listing 4.14 .

Listing 4.14 arithmetic expression tree usage examples

1 #include

2 #include "Node.h"

3

4 void main()

5 {

6 Node node1 = newNumNode(20.0);

7 Node node2 = newNumNode(-10.0);

8 Node node3 = newAddNode(&node1, &node2);

9 Node node4 = newNumNode(0.1);

10 Node node5 = newMultNode(&node3, &node4);

11 printf("Calculating the tree");

12 double x = Calc(&node5);

13 printf("Result:%lf", x);

14 }

2. Abstract class

According to the description of the problem, there is a set of such concepts in the demand vocabulary, such as the root node and the operands of the left and right leaf nodes, and the addition and multiplication are binary operations. Although the vocabulary corresponds to Node, _pLeft, _pRight, Number, Binary, Additive, and Multiplicative, it is more accurate to describe the nodes of the expression arithmetic tree with Node, _pLeft, _pRight, NumNode, BinNode, AddNode, and MultNode.

Since both AddNode and MultNode are binary operations, the commonality is the calculation of two numbers (_pLeft and _pRight) whose variability is addition and multiplication, respectively, so their commonality can be included in BinNode, and the variability is included in AddNode and MultNode.

In fact, the input operand can also be regarded as a calculation. Therefore, the commonality between NumNode and BinNode is also computation. It is possible to move their commonality up to the Node abstract class.

Obviously, based on object-oriented C programming, all nodes of the expression arithmetic tree are subclasses inherited from the class Node. The immediate descendants of Node are NumNode and BinNode, NumNode represents a number, BinNode represents a binary operation, and then Then derive two classes from BinNode: AddNode and MultNode.

As shown in Figure 4.7 shows the class hierarchy, which is an "is-a" hierarchy of abstraction, and subclasses AddNode MultNode redefined BinNode structure and behavior and the Node base class. The base class represents a generalized abstraction, and the subclass represents a special abstraction. Although the abstract class Node or BinNode cannot be instantiated and can only be used as a parent class of other classes, the NumNode, AddNode, and MultNode subclasses can be instantiated.

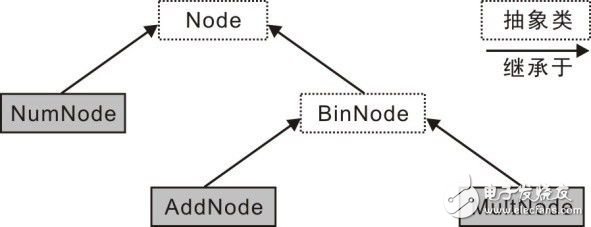
Figure 4.7 Class hierarchy of nodes

The Node abstract class is defined as follows:

1 typedef struct _Node{

2 double (*nodeCalc)(struct _Node *pThis);

3 }Node;

In addition to Node, each subclass implements its own nodeCalc calculation method and returns a double precision as a computed node value. which is:

1 typedef struct _NumNode{

2 Node isa;

3 double _num;

4 }NumNode;

5

6 typedef struct _BinNode{

7 Node isa;

8 Node *_pLeft;

9 Node *_pRight;

10 }BinNode;

11

12 typedef struct _AddNode{

13 BinNode isa;

14 }AddNode;

15

16 typedef struct _MultNode{

17 BinNode isa;

18 }MultNode;

The NumNode node is separated from Node, and _num represents the value. BinNode is also separated from Node. _pLeft and _pRight are pointers to the left and right subtrees respectively, and AddNode and MultNode are separated from BinNode.

Previously, for inheritance and polymorphic frameworks, an initialization paradigm called static was used. Here, the dynamic memory allocation initialization paradigm will be used to handle inheritance and polymorphic frameworks.

3. Establish an interface

Because the objects are different, the way to dynamically allocate memory is different, but the commonality is that when you no longer use an object, the method of releasing dynamic memory is the same, so you need to add a node_cleanup() function, which is through free( For implementation, see Listing 4.15 .

Listing 4.15 arithmetic expression tree interface (CalcTree1.h)

1 #pragma once

2 typedef struct _Node Node;

3 typedef double (*node_calc_t)(Node *pThis);

4 typedef void (*node_cleanup_t)(Node *pThis);

5 struct _Node{

6 node_calc_t node_calc;

7 node_cleanup_t node_cleanup;

8 };

9

10 typedef struct _NumNode{

11 Node isa;

12 double _num;

13 }NumNode;

14

15 typedef struct _BinNode{

16 Node isa;

17 Node *_pLeft;

18 Node *_pRight;

19 }BinNode;

20

21 typedef struct _AddNode{

22 BinNode isa;

23 }AddNode;

twenty four

25 typedef struct _MultNode{

26 BinNode isa;

27 }MultNode;

28

29 NumNode * newNumNode(double num);

30 double node_calc(Node *pThis);

31 AddNode * newAddNode(Node *pLeft, Node *pRight);

32 MultNode * newMultNode(Node *pLeft, Node *pRight);

33 void node_cleanup(Node *pThis);

The first step in implementing the expression arithmetic tree is to enter the data and initialize the variables isa and _num of the NumNode structure. The prototype of the newNumNode() function is as follows:

NumNode * newNumNode(double num);

The form of its call is as follows:

Node * pNode1 = (Node *) newNumNode(20.0);

Node * pNode2 = (Node *) newNumNode(-10.0);

The next step is to prepare for the calculation. The prototype of the node_calc() function is as follows:

Double node_calc(Node *pThis);

The form of its call is as follows:

Node_calc(pNode1);

Then start the addition, the newAddNode() function prototype is as follows:

AddNode * newAddNode(Node *pLeft, Node *pRight);

The form of its call is as follows:

Node * pNode3 = (Node *) newAddNode(pNode1, pNode2);

Of course, you can also start multiplication. The newMultNode() function prototype is as follows:

MultNode * newMultNode(Node *pLeft, Node *pRight);

The form of its call is as follows:

Node * pNode4 = (Node *) newNumNode(0.1);

Node * pNode5 = (Node *) newMultNode(pNode3, pNode4);

When everything is ready, the final result is calculated and the resources that are no longer used are released. The prototype of the node_cleanup() function is as follows:

Void node_cleanup(Node *pThis);

The form of its call is as follows:

Printf("Calculating the tree");

Double x = node_calc(pNode5);

Printf("Result:%lf", x);

Node_cleanup(pNode5);

4. Implement the interface

Obviously, after creating the corresponding class for each node, you can create a dynamic variable for each node, you can use malloc () to allocate memory at runtime and use pointer to store the address, and use pointer initialization The implementation of the CalcTree1.c interface for each member of the structure is detailed in Listing 4.16 .

Listing 4.16 implement arithmetic expression tree interface (CalcTree1.c)

1 #include

2 #include

3 #include " CalcTree1.h "

4

5 NumNode * newNumNode(double num)

6 {

7 NumNode *pNumNode = malloc(sizeof(NumNode));

8 if(pNumNode != NULL){

9 pNumNode -> isa.node_calc = _numnode_calc;

10 pNumNode -> isa.node_cleanup = _numnode_cleanup;

11 pNumNode -> _num = num;

12 }

13 return pNumNode;

14 }

15

16 static double _numnode_calc(Node *pThis)

17 {

18 printf("numeric node %lf", ((NumNode *) pThis) -> _num);

19 return ((NumNode *)pThis) -> _num;

20 }

twenty one

22 static void _numnode_cleanup(Node *pThis)

twenty three {

24 printf("NumNode cleanup");

25 free(pThis);

26 }

27

28 double node_calc(Node *pThis)

29 {

30 return pThis -> node_calc(pThis);

31 }

32

33 AddNode * newAddNode(Node *pLeft, Node *pRight)

34 {

35 AddNode *pAddNode = malloc(sizeof(AddNode));

36 if(pAddNode != NULL){

37 pAddNode -> isa.isa.node_calc =_addnode_calc;

38 pAddNode -> isa.isa.node_cleanup = _binnode_cleanup;

39 pAddNode -> isa._pLeft = pLeft;

40 pAddNode -> isa._pRight = pRight;

41 }

42 return pAddNode;

43 }

44

45 static double _addnode_calc(Node *pThis)

46 {

47 printf("Adding...");

48 AddNode * pAddNode = (AddNode*)pThis;

49 return node_calc(pAddNode -> isa._pLeft) + node_calc(pAddNode -> isa._pRight);

50 }

51

52 static double _multnode_calc(Node *pThis)

53 {

54 printf("Multiplying...");

55 MultNode * pMultNode = (MultNode*)pThis;

56 return node_calc(pMultNode -> isa._pLeft)*node_calc(pMultNode -> isa._pRight);

57 }

58

59 static void _binnode_cleanup(Node *pThis)

60 {

61 printf("BinNode cleanup");

62 BinNode * pBinNode = (BinNode*)pThis;

63 node_cleanup(pBinNode ->_pLeft);

64 node_cleanup(pBinNode ->_pRight);

65 free(pThis);

66 }

67

68 MultNode * newMultNode(Node *pLeft, Node *pRight)

69 {

70 MultNode *pMultNode = malloc(sizeof(MultNode));

71 if(pMultNode != NULL){

72 pMultNode -> isa.isa.node_calc = _multnode_calc;

73 pMultNode -> isa.isa.node_cleanup = _binnode_cleanup;

74 pMultNode -> isa._pLeft = pLeft;

75 pMultNode -> isa._pRight = pRight;

76 }

77 return pMultNode;

78 }

79

80 void node_cleanup(Node *pThis)

81 {

82 pThis -> node_cleanup(pThis);

83 }

> > > 1.1.3 virtual function

Although you can use inheritance to implement an expression arithmetic tree, each object in the implementation code has a function pointer. If there are many function pointers in the structure, or more objects must be generated, multiple objects will have the same behavior, require more function pointers, and need to generate a larger number of objects, which will waste a lot of memory.

You can transfer a member of Node to another struct to implement a virtual function table, and then create an abstract data type NodeVTable in the interface, on this basis, define a pointer vtable pointing to the table. such as:

1 / / interface (CalcTree2.h)

2 typedef struct _NodeVTable NodeVTable;

3 typedef struct _Node{

4 const NodeVTable * vtable;

5 }Node;

6 // Implementation (CalcTree2.c)

7 typedef double (*node_calc_t)(Node *pThis);

8 typedef void (*node_cleanup_t)(Node *pThis);

9 struct _NodeVTable{

10 const node_calc_t node_calc;

11 const node_cleanup_t node_cleanup;

12 };

13 const NodeVTable _addnode_vtable = { _addnode_calc, _binnode_cleanup};

The interface of the expression arithmetic tree is shown in Listing 4.17 , where NumNode is derived from Node, _num represents the value; BinNode is also derived from Node, pLeft and pRight represent pointers to the left and right subtrees respectively; and AddNode and MultNode are Derived from BinNode. Although an abstract class contains one or more pure virtual function classes, it cannot be instantiated (such objects have no objects to create), only classes derived from an abstract class and classes that provide implementation code for all pure virtual functions can be instantiated, They must all provide their own calculation methods node_calc and node_cleanup.

Listing 4.17 arithmetic expression tree interfaces (CalcTree2.h)

1 #pragma once

2

3 typedef struct _NodeVTable NodeVTable;

4 typedef struct _Node{

5 const NodeVTable * vtable;

6 }Node;

7

8 typedef struct _NumNode{

9 Node isa;

10 double _num;

11 }NumNode;

12

13 typedef struct _AddNode{

14 Node isa;

15 Node *_pLeft;

16 Node *_pRight;

17 }AddNode;

18

19 typedef struct _MultNode{

20 Node isa;

21 Node *_pLeft;

22 Node *_pRight;

23 }MultNode;

twenty four

25 double node_calc(Node *pThis);

26 void node_cleanup(Node *pThis);

27

28 NumNode * newNumNode(double num);

29 AddNode * newAddNode(Node *pLeft, Node *pRight);

30 MultNode * newMultNode(Node *pLeft, Node *pRight);

Obviously, after creating the corresponding class for each node, you can create a dynamic variable for each node, you can use malloc () to allocate memory at runtime and use pointer to store the address, and use pointer initialization The implementation of the expression arithmetic tree interface for each member of the structure is detailed in Listing 4.18 .

Listing 4.18 implement arithmetic expression tree interface (CalcTree2.c)

1 #include

2 #include

3 #include " CalcTree2.h "

4

5 typedef double (*node_calc_t)(Node *pThis);

6 typedef void (*node_cleanup_t)(Node *pThis);

7 struct _NodeVTable{

8 const node_calc_t node_calc;

9 const node_cleanup_t node_cleanup;

10 };

11

12 static double _numnode_calc(Node *pThis)

13 {

14 printf("numeric node %lf", ((NumNode *)pThis)->_num);

15 return ((NumNode *)pThis) ->_num;

16 }

17

18 static void _numnode_cleanup(Node *pThis)

19 {

20 printf("NumNode cleanup");

21 free(pThis);

twenty two }

twenty three

24 const NodeVTable _numnode_vtable = {_numnode_calc, _numnode_cleanup};

25

26 static void _binnode_cleanup(Node *pThis)

27 {

28 printf("BinNode cleanup");

29 BinNode * pBinNode = (BinNode*)pThis;

30 node_cleanup(pBinNode ->_pLeft);

31 node_cleanup(pBinNode ->_pRight);

32 free(pThis);

33 }

34

35 static double _addnode_calc(Node *pThis)

36 {

37 printf("Adding...");

38 AddNode * pAddNode = (AddNode*)pThis;

39 return node_calc(pAddNode -> isa._pLeft) + node_calc(pAddNode -> isa._pRight);

40 }

41

42 const NodeVTable _addnode_vtable = { _addnode_calc, _binnode_cleanup };

43

44 static double _multnode_calc(Node *pThis)

45 {

46 printf("Multiplying...");

47 MultNode * pMultNode = (MultNode*)pThis;

48 return node_calc(pMultNode -> isa._pLeft)*node_calc(pMultNode -> isa._pRight);

49 }

50

51 const NodeVTable _multnode_vtable = { _multnode_calc, _binnode_cleanup };

52

53 NumNode * newNumNode(double num)

54 {

55 NumNode *pNumNode = malloc(sizeof(NumNode));

56 if(pNumNode != NULL){

57 pNumNode -> isa.vtable = &_numnode_vtable;

58 pNumNode -> _num = num;

59 }

60 return pNumNode; 60 return pNumNode;

61 }

62

63 AddNode * newAddNode(Node *pLeft, Node *pRight)

64 {

65 AddNode *pAddNode = malloc(sizeof(AddNode));

66 if(pAddNode != NULL){

67 pAddNode -> isa.isa.vtable = &_addnode_vtable;

68 pAddNode -> isa._pLeft = pLeft;

69 pAddNode -> isa._pRight = pRight;

70 }

71 return pAddNode;

72 }

73

74 MultNode * newMultNode(Node *pLeft, Node *pRight)

75 {

76 MultNode *pMultNode = malloc(sizeof(MultNode));

77 if(pMultNode != NULL){

78 pMultNode -> isa.isa.vtable = &_multnode_vtable;

79 pMultNode -> isa._pLeft = pLeft;

80 pMultNode -> isa._pRight = pRight;

81 }

82 return pMultNode;

83 }

84

85 double node_calc(Node *pThis)

86 {

87 return pThis -> vtable -> node_calc(pThis);

88 }

89

90 void node_cleanup(Node *pThis)

92 pThis -> vtable -> node_cleanup(pThis);

93 }